삼각함수곡선이해

삼각함수 부분을 공부하다 보면 많은 변환 공식들이 나옵니다. 하나하나 외우다 보면 많이 헷갈리는데, 그 변환 공식들은 외울 필요가 없습니다...

 

사인곡선과 코사인곡선 탄젠트곡선을 그리는 방법만 알면 됩니다.

 

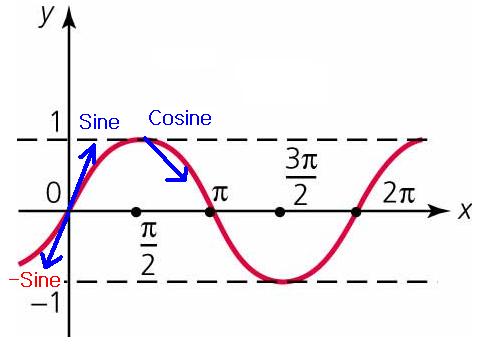
사인 함수 하나만 가지고 설명하겠습니다. (코사인과 탄젠트도 같은 방법으로 해결)  아래 그림에서 사인, 코사인, 사인 이라고 적어놓은 부분만 이해하면 변환 공식들이 모두 나옵니다.

 

 

위 그림을 설명하기 전에... 사인과 코사인의 차이가 뭘까요? 그건 바로 시작점의 y좌표가 0 과 1 이라는 것이죠. 사인은 0부터 시작하고 코사인은 1부터 시작합니다.

 

중요한 것은 두가지 입니다.

 

point 1.. 위 그래프가 사인함수인데도 불구하고 90도에서 출발한다고 보면 코사인 함수가 됩니다.. 90 도에서 음의 방향으로 출발하면 어떻게 될까요? 역시 코사인 함수가 됩니다. 반면 0, 180, 360 도에서 출발하면 사인 함수입니다.. (사인, 코사인의 결정..)

 

point 2..  만약 180도에서 오른쪽으로 움직인다고 생각하면 분명 0에서 출발하니 사인함수인데 음수니까 부호는 -가 됩니다. 180 도에서 되돌아오는 것은 그냥 사인함수 형태이므로 + , 270도에서는 어느 방향으로 가든지 -1부터 시작하니까 - (마이너스) .. (부호의 결정)

 

 

그럼 위 그림을 바탕으로 사인함수의 변환 공식을 구해보겠습니다..

 

sin ( 90 - θ )      ==> 사인함수의 90도에서 돌아오는 것이니까... cos θ 군요..

sin ( 90 + θ )     ==> 90 도에서 더 가는 것이니... cos θ 죠..

sin ( 180 + θ )   ==> 180 도에서 더가면 내려가는 사인함수니까...  - sin θ

sin ( 180 - θ )    ==> 180 도에서 돌아오니까 그냥... sin θ

sin ( 270 ± θ )  ==> 270 도에서 더가나 돌아오나 음의 코사인 ... -cos θ

 

이런 식으로 공식 유도가 가능합니다.. 하지만 공식을 유도하기 위해 이런 설명을 하는 것이 아니라 공식을 뛰어넘기 위해 이런 설명을 하는 것이기에 바로 실예로 들어가봅시다. 

 

sin 240 은 얼마일까요?

 

270 에서 30 만큼 되돌아오거나   ==> -cos 30

180 에서 60 만큼 더 가면 됩니다..==> -sin 60

 

간단하죠?

 

코사인과 탄젠트도 같은 방법입니다...

 

제가 이 부분을 공부할때 만들어서 썼던 방법인데 정석에 나오는 4사분면에서의 '얼싸안코' 보다 낫지 않나요?

 

한가지 단점....그래프가 머리속에 그려질때까지는 손으로 몇번 그려봐야 함. 

 

ps> 이 방법은 평행이동과 대칭이동의 개념을 삼각함수에 응용한 것입니다