삼각함수에 대한 이야기는 실제로 피타고라스 정리로부터 출발합니다. 피타고라스는 직각삼각형에서
변의 길이에 대해서 유명한 공식을 창안합니다.(빗변의 제곱은 나머지 두 변의 제곱의 합과 같다.)
피타고라스의 정리는 직각삼각형에 국한되는데 직각삼각형은 특수한 삼각형으로서 직각을 가지고 직각을
마주보는 변을 빗변이라고 하여 한 각에서의 높이/빗변값을 사인값, 밑변/빗변값을 코사인값, 높이/밑변값을 탄젠트값으로 정의했습니다. 이 때 사인 코사인 탄젠트는 0도부터 90도까지밖에 정의되지 않습니다. 지금까지는 중3의 삼각비 내용입니다.
고등학교 1학년 10나 마지막 단원 삼각함수는 삼각비의 내용을 90도 이상 또는 0도 이하로 모든 각도로 확장시
킵니다. 이를 위해 사인값과 코사인값, 탄젠트값 또한 삼각비의 내용을 포함하는 새로운 방법으로 정의합니다.
좌표평면에서 중심을 원점으로 하고 반지름이 1인 원을 단위원이라고 합니다. 단위원 위의 한 점 P(x,y)를
잡을 때 P의 x좌표를 코사인값, P의 y좌표를 사인값으로 하고 각 값의 대응되는 각도는 동경과 시초선 사이의
각으로 정의합니다.(동경과 시초선의 정의는 책을 참고하세요) 탄젠트값은 사인값/코사인값으로 정의합니다.
이 때 0도, 즉 시초선에서 사분면을 정하는 방향인 시계 반대 방향을 양(+)의 방향으로 정의하고 반대로 시초선에서 시계방향을 음(-)의 방향으로 정의합니다. 예를 들어 시초선에서 시계반대방향으로 30도 회전하면 +30도,
시계방향으로 60도 회전하면 -60도입니다. 지금까지는 삼각함수에서의 사인값, 코사인값, 탄젠트값의 정의와
이용 도구를 설명했습니다.
중학수학과 10나에서 함수를 다룹니다. 이 때 함수는 'y=x에 대한 관계식' 꼴로 주로 양함수를 배웁니다.
하지만 이러한 것은 수학의 함수라는 분야에서 일부분에 불과하며 음함수, 삼각함수 등 낯선 모양을 한
함수 역시 존재합니다. 삼각함수 역시 그런 부류로서, 동경이 시초선으로부터 어느 방향으로 몇도 회전했는
지에 따라 동경과 단위원의 교점은 반드시 1개씩만 대응되기 때문에 동경의 회전각을 정의역으로 하고
교점의 좌표를 치역으로 하는 함수를 생각할 수 있습니다. 만약 동경의 회전각을 정의역으로 하고 단위원과 동경의 교점의 y좌표를 치역으로 한다면 사인함수, x좌표를 치역으로 한다면 코사인함수, 교점의 좌표 중 y좌표/x좌표값을 치역으로 한다면 탄젠트한수입니다. 사인함수, 코사인함수, 탄젠트함수를 통틀어 삼각함수라고 하는 것입니다. 중3때 배우는 삼각비는 정의역이 0도와 90도 사이로만 제한된 특수한 경우의 삼각함수로 볼 수 있습니다.
삼각함수를 배우는 과정에서 호도법을 배웁니다. 호도법은 완전 새로운 것이 아니라 단지 각을 정의하는 또다른 방법에 불과합니다. 초등학교때부터 우리는 180도를 180등분하는 60분법을 사용해 왔습니다. 하지만 삼각함수는 호도법을 많이 사용합니다.(호도법의 정의 역시 책에 잘 나와 있습니다.)
삼각함수가 낯선 호도법을 사용하는 이유는 삼각함수의 특징을 이용하기 위해서입니다. 사인과 코사인함수는
2파이(360도)마다 같은 그래프가 되풀이되고 탄젠트함수는 파이(180도)마다 되풀이되는 주기함수입니다. 그런데 삼각함수는 초월함수라는 큰 범주에 속하는데 초월함수는 한 정의역에 대응되는 일반적인 치역값을 구하기가 굉장히 어렵다는 특징이 있습니다. 그 결과 고등학교 과정에서는 30도, 60도, 90도, 120도, 150도 등 특수한 각에 대한 값을 구해놓고 계속 그 각으로만 삼각함수를 다루게 됩니다.(학생은 계산을 빠르게 하기 위해 대응하는 삼각함수의 각을 외워서 사용하는게 일반적입니다. 실제로 문제도 그렇게밖에 나오지 않으니까요)
30도는 호도법으로 파이/6이 되는데 만약 분모가 6인 값을 정의역으로 하는 사인함수를 다루게 된다면 대하기 이상한 각을 30도의 각으로 변환하여 사인30도의 값으로 바꿔서 계산할 수 있습니다.
예를 들어 570도는 고등학교에서 흔히 다루는 각이 아니고 사인 570도를 구하기가 매우 어렵습니다. 하지만
570도는 호도법으로 바꾸면 파이/2의 3배에 파이/6입니다. 파이/2, 즉 직각을 제외한 각이 30도이므로 변환한 최종각은 30도임을 알 수 있습니다. 실제로 직각의 3배 즉 홀수배이므로 사인이 코사인으로 바뀌고, 4사분면에서 사인값은 음수이므로 값의 부호가 바뀌게 됩니다. 즉, +사인570도는 -코사인30도입니다.
또다른 장점은 각의 표현이 간결하다는 것입니다. 우리가 60분법을 편히 느끼는 것은 원래부터 그리 어렵지 않은 각을 다루기 때문입니다. 하지만 우리가 다루는 각이 만약 36382도같이 허무맹랑한, 어디서 본적도 없는 값이면 말 그대로 이게 뭐꼬? 입니다. 그런데 이를 호도법으로 다루게 되면 이 각은 하나의 기약분수에 파이를 곱한 꼴로 바뀌게 됩니다. 그 기약분수는 1/2의 배수형태 + 또다른 기약분수로 나타낼 수 있습니다. 이렇게 바꾸면 1/2파이는 직각이므로 사라지게 되는데 다시 말해 아무리 크고 요사스런 각을 다룬다고 해도 우리가 알아보기 쉬운 작은 각으로 바꿀 수 있습니다.
이렇듯 60분법보다 호도법이 삼각함수의 특징을 이용해서 큰 각을 작은 각으로 만들 수 있기 때문에 삼각함수에서 호도법을 많이 사용합니다.
삼각함수에 대한 문제는 고등학교 수준에서 크게 4가지로 나눌 수 있습니다.
1. 사인값, 코사인값, 탄젠트값의 특징을 이용한 삼각함수값들 끼리의 계산
2. 삼각함수의 정의를 이용하여 실생활 문제 해결 (길이구하기, 각도구하기, 넓이구하기)
3. 삼각함수값 사이의 여러가지 변환
4. 무슨 방법이든 여러가지 요사스런 꼼수를 사용하여 문제풀기(통합문제)
로 볼 수 있습니다. 1,2번은 중3~고1수준, 3,4번은 심화 미분과 적분을 배운 학생 수준입니다.
1,2번 수준 문제.
한 사람이 강가를 걷고 있었다. 강 건너편 강가에는 강으로 곧장 떨어지는 폭포가 있었는데 갑자기 그 사람은
폭포의 높이를 알고 싶어했다.(이유는 묻지마라. 그냥 알고싶은거다.)
하지만 그는 강의 넓이도 모른다. 그 사람이 지금 자와 각도기를 가지고 있다면 폭포의 높이를 구하는
방법을 설계하라. (폭포와 강 사이의 거리는 무시하고 그가 길이를 잴 수 있는 한계는 없다고 하자. 또한
그는 자리를 이동하여 각도를 잴 수 있다. 강의 폭은 일정하다고 가정한다.)
3,4번 수준 문제.
좌표평면에 한 점에서 만나는 두 직선이 있다고 하자. 두 직선이 교차할 때 이루는 각의 탄젠트값을 구하여라.
(두 직선은 서로 한 점에서 만나는 모든 직선을 대상으로 하며, 모든 경우에서 각의 탄젠트값을 알 수 있는 방법을
제시하여라.)
1,2번 문제 풀이.
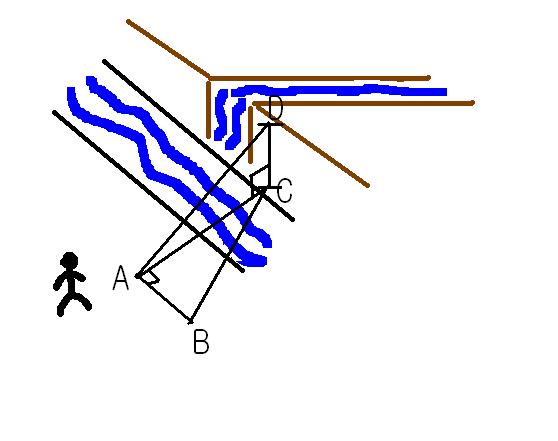
폭포의 높이는 선분 DC이다. 그 사람은 선분 AB의 길이를 구할 수 있고 각 CBA를 구할 수 있다. 탄젠트CBA는
CA/AB이므로 AB의 길이와 탄젠트 CBA의 곱은 선분 CA의 값이다. 또 그 사람은 각 DAC를 구할 수 있으므로
같은 원리에 의해 선분 AC의 곱과 탄젠트 DAC의 곱이 선분 DC의 값, 즉 그 사람이 원하는 폭포의 높이이다.
3,4번 수준 문제 풀이
좌표평면에서 직선의 기울기의 정의는 y증분/x증분이다. 직선 위에서 서로 다른 두 점을 잡을 때 두 점 사이 선분을 빗변으로 하고 각 점을 지나고 X축, Y축과 평행한 직선을 그을 수 있다. 서로 다른 두 점을 잡을 때는 X값이 작은 점을 A라고 놓고 X값이 큰 점을 B라고 놓는다. A점에서의 X증분의 길이를 밑변으로 하고 A값에서의 Y증분의 길이를 높이로 하는 직각삼각형을 생각할 때 직각부분을 C라고 놓는다면 탄젠트 BAC는 y증분/x증분값과 일치한다. 그런데 y증분/x증분값은 그 직선의 기울기이므로 탄젠트 BAC는 그 직선의 기울기이다. 그런데 각 BAC는 평행이동해서 그 직선과 X축의 양의 방향과 이루는 각으로 볼 수 있으므로 그 직선과 X축의 양의 방향으로 이루는 각의 탄젠트값은 그 직선의 기울기이다.
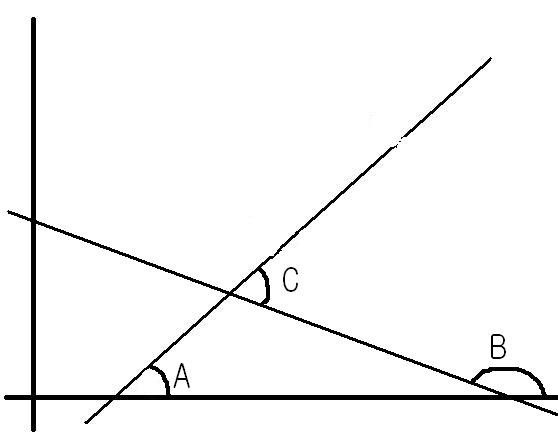
좌표평면에서 두 직선이 이루는 각은 C이다. 그런데 C는 각 A와 각 180도-B의 합이다.(삼각형의 한 외각은 다른 두 내각의 합이므로)
따라서 tan{A+(180-B)}=tanC이다.
tan{A+(180-B)}=tan(A-B)=
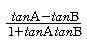
이다. tanA와 tanB는 각각 두 직선의 기울기값이므로 tan(A-B)는 두 직선이 이루는 각의 탄젠트값이다.