사인(sine: sin): 정현(正弦)
코사인(cosine: cos): 여현(餘弦)
탄젠트(tangent: tan): 정접(正接)
코시컨트(cosecant: cosec, csc): 여할(餘割)
시컨트(secant: sec): 정할(正割)
코탄젠트(cotangent: cot): 여접(餘接)
사인 함수 sine의 어원은 원호의 현(弦, chord)과 관계 있다. 지름이 1인 원 안에 내접하면서, 지름을 빗변으로 하는 직각삼각형이 있다고 생각할 때 직각이 아닌 어떤 각과 마주보는 변(원에 내접하므로 원호의 현도 된다)의 길이는 사인 값이 되고, 나머지 한 변의 길이는 코사인 값이 된다는 것을 연상하면 된다. 아울러 접두사 코(co)는 '부수적인 것, 나머지'라는 의미를 나타내어서 코가 붙는 것들은 모두 나머지 여(餘)를 붙인다. 그래서 사인 값을 나타내는 현을 기준으로 한다면 정현이고, 코사인은 여현이다.
사인 함수가 sine이 된 것은 실제로는 오역에서 비롯된 것이다. sine은 라틴어 sinus(시누스)에서 나온 것인데 이 말은 '옷의 주름, 접힘' 같은 뜻을 나타내고 삼각함수나 원호의 현과는 직접 무관하다. 1150년경 이탈리아 수학자 게라르도(Gherardo of Cremona)가 아랍어 수학 책을 번역하면서 아랍어로 현이나 사인 함수를 나타나는 jiba(지바)를 옷의 주름을 가리키는 jaib(자이브)와 혼동해서 sinus로 옮긴 데서 사인 함수가 sinus, 여기서 영어로 sine이 된 것이다.
탄젠트가 접(接) 자를 써서 정접이 된 것은 접선(接線)을 나타낸다는 것과 관계 있다. 접선을 영어로는 tangent line, 또는 그냥 줄여서 tangent로 쓰고, 직선의 각도를 알 때 직선의 기울기는 탄젠트 값으로 주어진다. 코탄젠트 역시 탄젠트를 기준으로 할 때 부수적인 양이 된다는 데서 나온 것이다.
탄젠트는 원래는 사인이나 코사인처럼 각도에 대한 함수가 아니라 어떤 물체의 그림자 길이에서 높이를 계산하는 데서 고안된 것이다. 그래서 중세에는 움브라 렉타(umbra recta: 바른 그림자, 수직으로 세운 막대가 수평면에 드리우는 그림자)와 움브라 베르사(umbra versa: 반대 그림자, 수평으로 된 막대가 수직면에 드리우는 그림자)와 같이 그림자와 관련된 이름으로 불렸으며(이들 라틴어 이름도 아랍어 책을 번역하면서 만들어진 것이다), 이 개념을 접선의 기울기와 연관지어 탄젠트라고 부른 것은 덴마크 수학자 토마스 핀케(Thomas Fincke, 1561-1656)가 최초이다.
시컨트가 할(割) 자를 써서 정할이 된 것은 할선(割線: 원과 두 점에서 만나는 직선)과 관계 있다. 할선을 영어로는 secant line, 또는 그냥 줄여서 secant라고 하고, (원의 지름)/(할선이 이루는 현의 길이)를 구하면 할선이 만드는 현과 지름 사이에 끼인 각에 대한 시컨트 값이 된다. 코시컨트 역시 시컨트를 기준으로 할 때 부수적인 양이 된다는 데서 나온 것이다.
상수 e 의 이야기
수 e는 수학적 중요도로 볼 때 원주율(파이)와 대등하고, 통상 얌전한 영어 소문자로 쓰여져 친숙한 느낌을 주는, 하지만 그래도 그 속을 이해하기가 보통 쉽지 않은 자연로그의 밑수 e는 대략 그 값이 2.718281828459045235360287471352662497이다.
상수 e는 18세기 중엽에 스위스의 수학자 오일러가 처음으로 세상에 소개한 수이다. 상수 e에 대한 표준적 정의를 처음 접하는 사람에게는 그 정의가 약간 복잡하고 어렵게 보일지 모른다.
수 e는 '정수 N이 점점 커질 때, 일반항이
인 수열의 극한값'으로 정의된다. N이 2일 때, 위의 식은
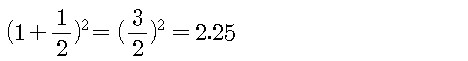
가 된다. N이 3일 때 그것은
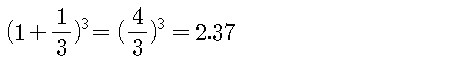
이고, N의 값이 연속적으로 커짐에 따라 차례로
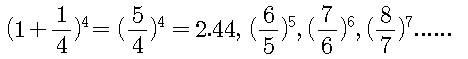
이렇게 계속된다. 따라서 e는
와 아주 가깝다. 또한 상수 e는
에 더 가깝다.
비록 정의가 추상적이기는 하지만 이와 같이 e를 정의하면, 우리는 은행의 서류나 복리계산에 빠짐없이 나오는 e의 중요한 역할을 눈치챌 수가 있다.
e는 자연로그 함수의 밑수이다. 이 말을 명확이 이해하려면 까다로운 로그에 대한 약간의 부연 설명이 필요하다.
예를 들어, 10의 제곱은 100이므로 100의 상용로그는 2이다. 10의 세제곱은 1000이므로 1000의 상용로그는 3이다. 그리고 10의 2.7제곱은 500이므로 상용로그는 2.7이다. [log(500)=2.7]
한편, 어떤 수의 자연로그는 그 수와 같아지는 e의 지수를 나타낸다. 따라서, e의 (6.9)제곱은 1000이므로 1000의 자연로그는 (6.9)가 된다. [ln(1000)=6.9]
e의 (4.6)제곱은 100이므로 100의 자연로그는 (4.6)이고, e의 (0.7)제곱은 2이므로 2의 자연로그는 0.7이다. 특히 마지막 수 2의 자연로그인 (0.7)은 재정학에서 매우 중요하다.
상수 (0.7)을 당신이 받는 이율로 나눈 값이 바로 당신의 원금이 두 배가 되는 데 걸리는 년수가 된다. 따라서 이율이 10%(0.10)일 때 당신의 원금이 두 배가 되는 데 걸리는 년수는 7년(0.7을 0.1로 나눈값)이고, 이율이 14%이면 원금이 두 배가 되는 년수는 5년(0.7을 0.14로 나눈값)이다.
이제부터 상수 e가 연출하는 믿기지 않는 현상을 몇 가지만 살펴보자. 우선 부교수를 1명 채용하고자 N명의 후보를 면접해야 하는 S대학 M학과가 있는데, 그 학과는 아래의 3가지 면접 원칙을 가지고 있다고 하자.
첫째, 후보의 면접이 끝나는 즉시 당사자에게 채용 여부를 알린다.
둘째, 일단 면접에서 떨어진 사람을 다시 면접해서 채용할 수는 없다.
셋째, 면접이 마지막 사람까지 가면 그는 자동적으로 채용된다.
이 3가지 면접 원칙으로 M학과는 과연 자신이 원하는 최선의 후보를 채용할 수 있을까? M학과가 최선의 후보를 채용할지 여부는 아무도 장담할 수 없다. 그러나 M학과는 자신이 원하는 최선의 호보를 채용할 수 있는 확률은 극대화할 수 있는데, 그 전략은 통상 다음과 같이 세워진다.
먼저 Kn 따라서 만약 40명의 후보를 무작위 순서로 면접한다면 최적의 전략은 즉석에서 40명의 37%인 처음 15명을 무조건 떨어뜨린 다음 그의 앞 사람 모두보다 더 나은 후보를 부교수로 채용하는 것이다. 이런 방법을 사용해서 최선의 후보를 채용하게 될 확률 또한 아주 이상하게 1/e 또는 약 37%이다. 어떤 전략도 37%보다 더 좋은 확률을 가져다 주진 않는다. 비록 전제 조건인 M학과의 면접 원칙에 부자연스러운 면이 없진 않지만, 배우자를 선택하기 위한 '맛선 보기'와 같은 유사한 문제들 역시 이와 동일한 접근법과 논법이 사용된다.
상수 e는 무리수(두 정수의 비로 나타낼 수 없기 때문에 비순환 무한소수)인 동시에 초월수(대수방정식의 근이 될 수 없는 수)이다. 그럼에도 불구하고 e는 중요한 수학공식과 정리에 매우 흔하게 나타난다. 수 e는 삼각함수, 기하학, 미분방정식, 무한급수, 해석학 등 무수히 많은 서로 다른 수학의 분야에서 항상 필수적으로 등장하는 참으로 신출귀몰하고 의미심장한 수이다.
밤 12시에 받은 전화한통때문에, 생각도 안나고, 배운거 같은데 기억은 안나고..-_-;;;;
문제는,
을 호도법을 이용해서 풀어라.
위는 고등학교 미적분에 나온 내용으로, 로피탈 정리를 쓰면 아주 간단히 해결 가능한 문제이다. 이를 호도법으로는 어떻게 풀것인가?
허접한 그림 하나-_-;;;; 뭐, 알아먹을 정도이니, 양호하다...ㅋㅋ
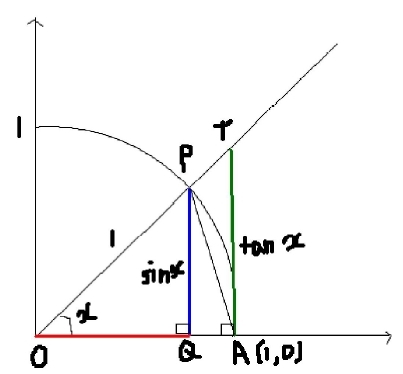
면적을 비교해보면, (*)----
면적 △OAP = 1/2 sin(x) 부채꼴 OAP = 1/2 *x 면적 △OAT = 1/2 tan(x)
그래서, 1/2 sin(x) < 1/2*x <1/2 tan(x) 이고, 양변을 1/2 * sin(x) 로 나누면, 1 < x / sin(x) < 1 / cos(x) 이므로, 역수를 취하면, 1 > sin (x) / x > cos (x) 이다. 이를 극한을 취하면, lim cos(x) =1 as x->0+ 이고, 그래서 , lim sin(x) / x = 1 as x ->0+ 이다.
한편, sin(x) 함수는 우함수이므로, lim sin(x)/x =1 as x->0 이므로, 증명 |
★lim (sinx/x) =1 을 호도법으로 증명하자.
| 질문: 등속운동에서 그래프 아랫부분의 면적=이동거리인 이유 | kayla220 / 2008-01-18 00:52 |
|
| |
| 답변: re: 등속운동에서 그래프 아랫부분의 면적=이동거리인 이유 | to1992 / 2008-01-18 01:05 |
|
중학교에 다닐 때 배우는 '일차함수'에 나오는 내용입니다.
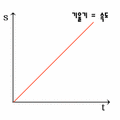
일차함수(일단 직선의 그래프라고만 알고 계셔요)의 그래프에서, 기울기를 구할 때에는, y축을 x축으로 나누어서 구합니다. (x분의 y)
그렇게 되면, 첫 번째 그래프의 답이 나옵니다. 기울기는 x축분의 y축, 즉 '시간'분의 '이동거리'입니다.
'시간'분의 '이동거리'는 '속력'이라는 사실 알고 계시죠? (거리=시간×속력)
두 번째 그래프에서는 면적을 구해야 하므로, 사각형의 넓이인 (가로×세로)를 하면 됩니다. 가로축의 '시간'과 세로축의 '속력'을 곱하면 '거리'가 됩니다. (시간×속력=거리) | |
[출처] [본문스크랩] 등속운동에서 그래프 아랫부분의 면적=이동거리인 이유|작성자 크게이룰 | |
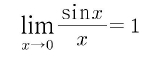
기울기=속력인 이유와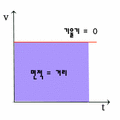
면적=이동거리인 이유좀 알려주세요~~